
This project presents a novel approach to investment decision-making under uncertainty, leveraging the First-Order Stochastic Dominance (FSD) and Second-Order Stochastic Dominance (SSD) criteria. The primary objective is to optimize the selection of investments in high-risk scenarios.
The innovative aspect of this project lies in the development of a method that combines or convolves two investment functions. This approach aims to balance the trade-off between risk and return, striving to maximize returns while minimizing risk. This is particularly applicable in cases where the two investments have discrete functions.
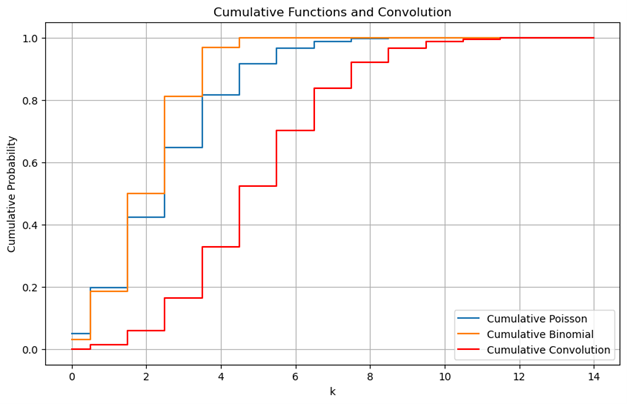
The image provided illustrates the application of this approach. It presents a graph titled “Cumulative Functions and Convolution,” displaying three cumulative probability functions: Cumulative Poisson (blue), Cumulative Binomial (orange), and Cumulative Convolution (red). The Cumulative Convolution function appears to be an integration or mix of the Poisson and Binomial functions, showcasing characteristics of both, which aligns with the project’s approach of mixing two investment functions.
Overall, this project contributes to the field of investment decision-making by providing a robust method for handling risky investments, potentially leading to more resilient and profitable investment strategies.
